Samsungs Dolby Atmos Surround Sound Alternative kommt noch in diesem Jahr
Samsungs IAMF-Format ermöglicht vertikalen und horizontalen Mehrkanal-Surround-Sound ähnlich wie Dolby Atmos, ohne dass dafür Lizenzgebühren anfallen.

Samsungs IAMF-Format ermöglicht vertikalen und horizontalen Mehrkanal-Surround-Sound ähnlich wie Dolby Atmos, ohne dass dafür Lizenzgebühren anfallen.
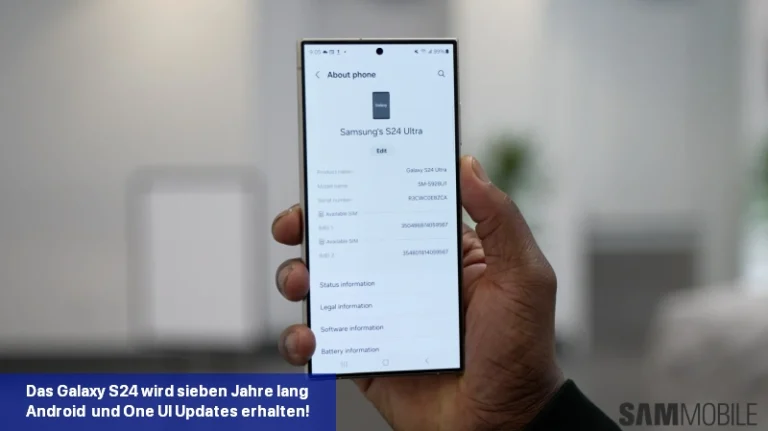
Samsung hat bestätigt, dass die Galaxy S24-Serie im Rahmen der Nachhaltigkeitsbemühungen des Unternehmens sieben Jahre lang Software-Updates erhalten wird.

Das Samsung Galaxy S23 FE erhält in Europa, Afrika und Lateinamerika das Sicherheitsupdate für Januar 2024.

Januar 2024 Unpacked ist in vollem Gange und Samsung hat gerade die Galaxy S24-Serie mit One UI 6.1 enthüllt. Die neue Software-Iteration basiert auf dem Betriebssystem Android 14, bringt aber wesentliche Verbesserungen gegenüber der One UI 6.1-Version. Samsung hat bestätigt, dass es das Galaxy AI-Erlebnis auf ausgewählte Galaxy-Geräte bringen wird […]
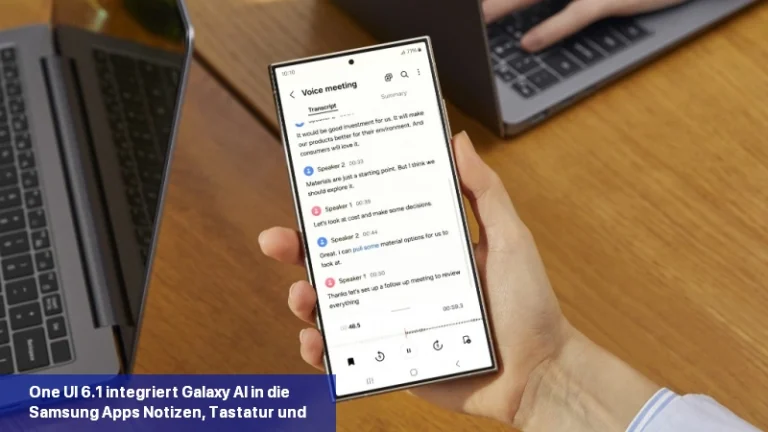
Galaxy AI soll die Art und Weise, wie Sie mit Ihrem Samsung-Gerät interagieren, revolutionieren. Die kürzlich vorgestellte Galaxy S24-Serie ist Samsungs erste KI-gestützte Produktreihe. Es ist interessant zu wissen, dass Googles KI-Modell Gemini Pro KI-Funktionen in die Samsung Galaxy S24-Smartphones einbringt. Samsung ist der erste Google Cloud-Partner, der Gemini Pro auf Vertex einsetzt […]

Wenn Sie wissen, wie Sie Ihren Spotify-Hörverlauf, auch bekannt als „kürzlich abgespielt“, anzeigen und löschen können, ist dies ein praktisches Tool für alle Situationen.

Die Samsung Health-App bietet mehrere nützliche Funktionen, die Ihnen bei der Verwaltung Ihrer Fitness und Ihres Wohlbefindens helfen, so dass Sie ganz einfach Ihre Ziele festlegen, Ihre Fortschritte überprüfen und alle Ihre Fitnessaktivitäten aufzeichnen können. Mehrere Galaxy-Nutzer haben kürzlich berichtet, dass sie die Samsung Health-App nicht richtig nutzen können, da sie abstürzt […]

Samsungs Galaxy S23 FE könnte das am besten geeignete Gerät für diejenigen sein, die ein Anti-Lag-Gaming-Erlebnis bevorzugen. Sie können ein Gerät haben, das nicht nur durch großartige Leistung unterstützt wird, sondern auch viele andere Funktionen, die das Spielerlebnis maximieren. Die Kombination aus fähiger Leistung, ausgeklügeltem Temperaturmanagement und guter Akkulaufzeit beweist […]

Das Samsung One UI 6.0 Update bringt das neue Android 14 OS auf die Galaxy-Geräte. Im August startete das Unternehmen das öffentliche Beta-Programm von One UI 6, mit einem stabilen Rollout begann Ende Oktober. Auf dieser Seite finden Sie alle nützlichen und aktuellen Informationen, die Sie über das große Update wissen sollten. Samsung One […]

One UI 6 ist das neueste Update für Samsung Galaxy-Smartphones und -Tablets, und hier sind alle neuen Funktionen und Änderungen in ihm! Probieren Sie es aus!
One UI 6 ist endlich für einige Nutzer vollständig verfügbar und bringt eine Reihe von Änderungen am Betriebssystem mit sich. One…

Samsung hat eine neunte Android 14-Beta für die Galaxy S23-Serie veröffentlicht, die genau zu dem Zeitpunkt kommt, zu dem die endgültige Version erwartet wird.

Das Samsung Galaxy S23 FE ist jetzt auf den Markt gekommen, aber das Gerät ist jetzt teurer als von Samsung angekündigt.

Mit jeder Generation hat Samsung seine faltbaren Geräte besser und robuster gemacht. Beim Galaxy Z Flip 5, das mit der neuesten Technologie ausgestattet ist, … MEHR LESEN

Samsungs faltbares Smartphone der nächsten Generation, das Galaxy Z Fold 5, kommt mit mehreren Kameraverbesserungen und Funktionen im Vergleich zu seinem Vorgänger. Samsung hat einige bedeutende … MEHR LESEN

Samsung hat das neueste Galaxy Z Flip 5-Gerät entwickelt, das sich an ein modernes und anspruchsvolles Publikum richtet und den Nutzern ein differenziertes und … LESEN SIE MEHR

Samsung sorgt bei jeder technologischen Innovation für effektive Änderungen und Verbesserungen, so auch bei den Galaxy Z Fold 5 Edge-Panels. Die Edge-Panels haben einige … MEHR LESEN
Haben Sie schon einmal Benachrichtigungen von Ihrem Smartphone-Bildschirm gelöscht oder weggewischt, um Ablenkungen zu vermeiden? Manchmal tun wir das, weil wir denken, es sei nicht nötig. … MEHR LESEN
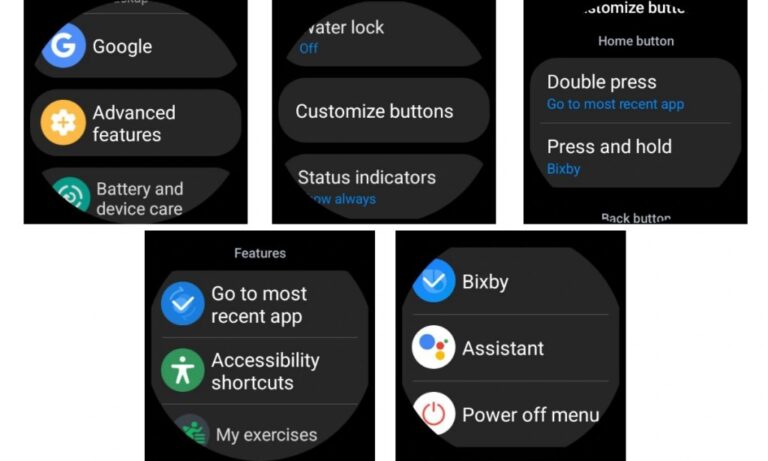
Eine der aufregendsten und praktischsten Funktionen ist die Anpassung, und Samsung Smartwatches sind da nicht anders. Samsungs hochgradig anpassbare One UI-Oberfläche bietet die Möglichkeit … LESEN SIE MEHR
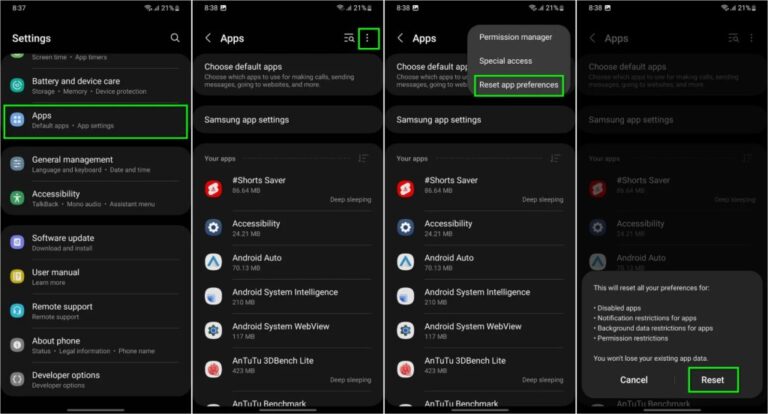
Ein Problem bei Samsung Messages verhinderte, dass bestimmte Galaxy-Smartphone-Nutzer auf die App zugreifen konnten. Samsung Messages ermöglicht es Einzelpersonen oder Gruppen, Nachrichten zu verfassen und zu planen … MEHR LESEN

Samsung ist sehr aktiv die Einführung der One UI 6 Beta-Update für die Galaxy-Geräte. Das Unternehmen initiierte das Beta-Programm für das Galaxy S23 Gerät zwei … MEHR LESEN
Haben Sie schon einmal mit Ihren Freunden über ein ganz bestimmtes Produkt gesprochen und es dann ein paar Stunden später in einer der Social-Media-Apps beworben gefunden? Nicht nur Sie. In den USA haben BDG Studios und OnePoll 1.000 GenZ befragt, um zu erfahren, wie sie mit Datenschutz- und Sicherheitsfragen auf ihren Telefonen umgehen. […]

Samsung bietet mit seiner Kamera-App eine Vielzahl von Funktionen für die Aufnahme von Fotos und Videos. Neben den vielen Fotomodus-Funktionen bietet Samsung eine erstaunliche Videomodus-Funktion namens „Auto Framing“ für Galaxy-Geräte an, mit der Sie professionell wirkende Videos aufnehmen können. Und mit der One UI 5.1 verbessert das Unternehmen die Auto Framing-Funktion um […]

Samsung hat endlich den Vorhang für das Galaxy Z Fold 5 und Z Flip 5 gelüftet, und wir haben die neuen faltbaren Geräte ausprobiert.

Wurde auf Ihrem Samsung Smartphone oder Tablet Feuchtigkeit erkannt, können Sie das Gerät nicht mehr laden. Wir zeigen Ihnen, wie Sie das Problem lösen.

In den letzten Jahren hat Samsung wiederholt für negative Presse durch lästige Werbung per Push-Benachrichtigungen gesorgt. Wir verraten Ihnen, was an den Vorwürfen wirklich dran ist.

WhatsApp hat offiziell die Chat-Sperre eingeführt. Ab heute können Samsung Galaxy-Nutzer von der brandneuen Chat-Sperre auf WhatsApp profitieren. Wenn sie aktiviert ist, schützt sie Ihre intimsten Unterhaltungen hinter einer weiteren Sicherheitsebene. Die beliebte Messenger-App verfügte bereits über eine biometrische Sperrfunktion, mit der Nutzer den Zugang für andere verhindern konnten. Inzwischen ist die Chat-Sperre […]
In dieser FAQ findest du eine Anleitung für die Aufnahme von Astrofotos und Mehrfachbelichtungen mit der Expert RAW App sowie einige hilfreiche Tipps.

Bei WhatsApp gibt es nicht nur individuelle Accounts, sondern auch „Business“ Accounts. Das sind WhatsApp-Konten, die…

TikTok ist überfüllt mit angenehmen, anregenden, humorvollen und spannenden Videos. Wenn dir ein bestimmtes Video besonders gut gefallen hat, du aber nicht…

Snapchat schließt sich dem Trend zur künstlichen Intelligenz an und führt „My AI“, einen Chatbot, auf der bekannten Social Media Plattform ein. Diese Funktion…
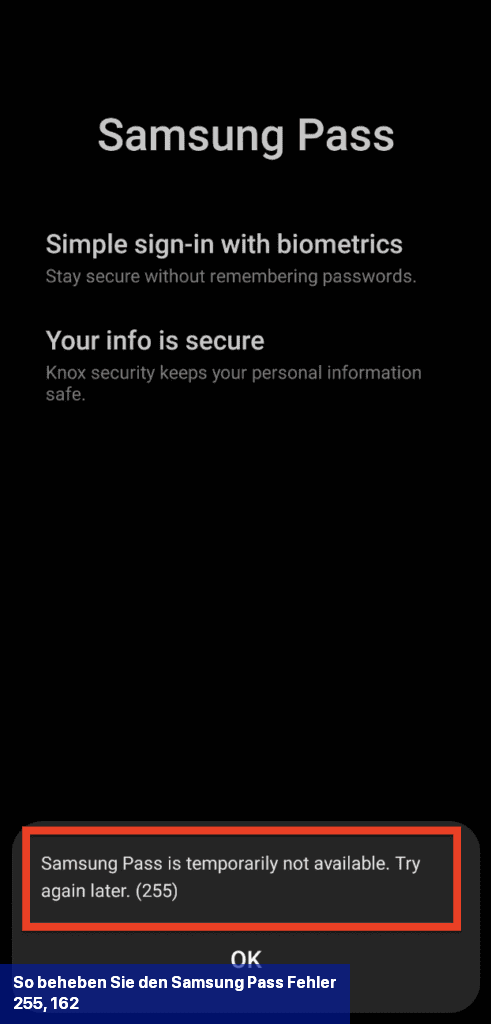
Eine der Lösungen zur Behebung des Samsung Pass-Fehlers 255 besteht darin, Wi-Fi zu deaktivieren und stattdessen das Mobilfunknetz Ihres Telefons zu verwenden.
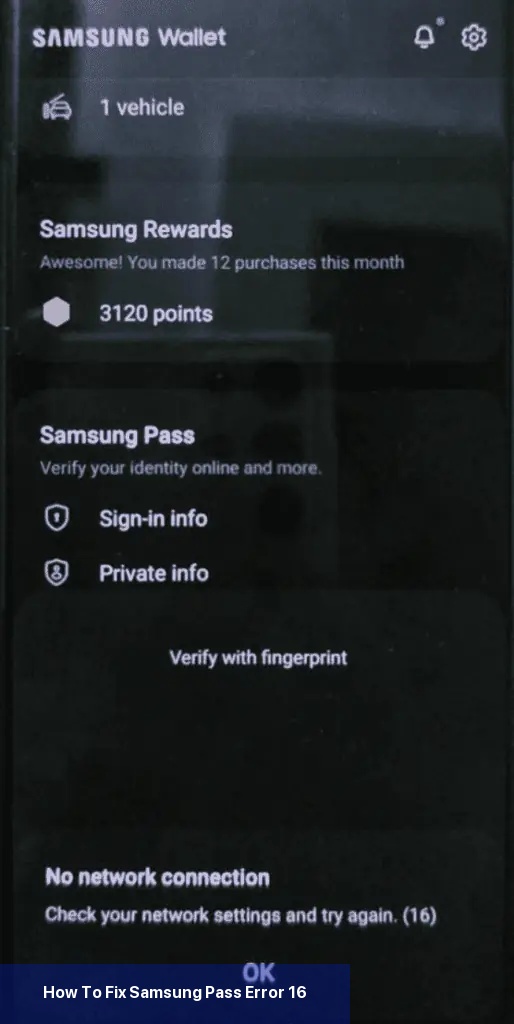
Das erste, was Sie tun sollten, um den Fehler 16 zu beheben, ist sicherzustellen, dass Ihr Telefon mit einer stabilen Internetverbindung verbunden ist. Wenn Sie mobile Daten verwenden, versuchen Sie, auf Wi-Fi umzuschalten, oder umgekehrt.
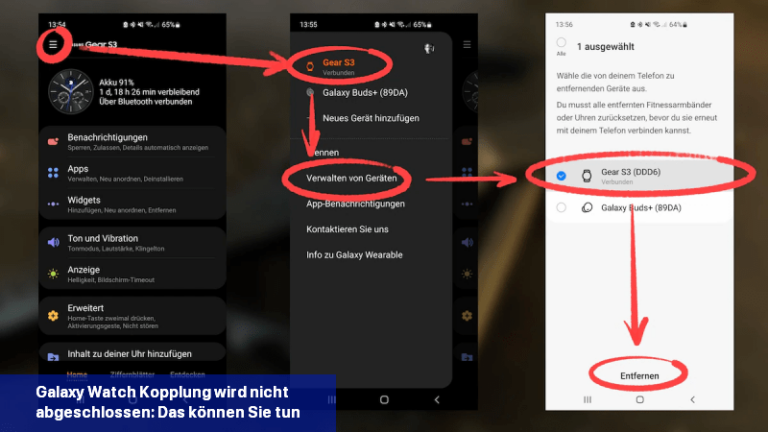
Wenn das Verbinden einer Galaxy Watch mit einem Mobiltelefon nicht funktioniert, kannst du versuchen, das Problem durch bestimmte Schritte zu beheben.

Wenn du deine Daten synchronisieren möchtest, kannst du Samsung Health mit Google fit verbinden. So kannst du gespeicherte Informationen verschieben.
Mit der Funktion „Message Guard“ von Samsung kannst du dich vor Gefahren auf deinem Mobiltelefon schützen. Wir erklären dir, wie sie funktioniert und wie du sie einsetzen kannst.